Imagine you are given a list of all transactions over the last 100 years. You want to download the details of each transaction from a service, but your API key allows you to query date ranges. Your provider bills you each time you make an API call. Being the shrewd scraper that you are, you want to spend as little money as possible.
“That’s easy,” you say. “Just make the date range cover the entire period with data and you’ll only need to make one API call. Boom!”
Unfortunately your service provider is a little clever, and also thinks that’s too easy. “If I can’t buy a Lamborghini every day, it’s not worth waking up in the morning!”. For fun and for profit, they cap each query to return at most 2 results per page, and 3 results per query.
Well shit, I guess we can’t just make a single API call then. Time to pony up a lambo? Well, maybe not just yet. This situation is very similar to the bin packing problem. Instead of minimising API calls, the bin packing problem wants to pack items into shipping containers, and minimise the number of containers you use (see 1-D bin packing problem). Another way to think of it is, if we put all the items in a line, how do we figure out where the cut off boundaries are so that we use the least number of containers to put the items into. It is part of a family of well studied problems that are “Knapsack-like”. Let’s take a look at an approach with dynamic programming.
Modelling the problem
The less mathematically inclined can skip this section. Having said that, it’s usually a good idea when dealing with a new problem to try and understand precisely what you are trying to solve. Writing down a concise description of the statement is a good start, and the language of mathematics is a great way to do it. We can think about the specific example described above, and generalise the limits.
In essence we are trying to minimise the number of API calls to make. Since each page has a maximum of 2 results, and there’s 3 maximum results per query, lets pretend you can have at most 3 results per day of transactions, i.e., the maximum number of required API calls is 3 per day. We can pretend the API calls are the items, and the API limits are the cargo containers. Let’s line up 2 containers for each day across the last 100 years. Let \(c_i \in \{0,1\}\) represent whether container \(i\) needs to be used. Then we are trying to minimise \(\sum c_i\) subject to some constraints.
What are the constraints?
Obviously we want to actually fetch all the data. So let \(r_i\) be the number of records fetched by \(c_i\), and \(N\) be the total number of records, then we need \(\sum r_i c_i = N\).
Next, we know each page or “container” can only hold at most 2 records, i.e., \(r_i \leq 2\). This means, if the limit was \(M\) instead, then we can represent this in the number of records fetched by adding the further constraint that \(r_i \leq M\).
Finally, each query can have at most 3 records, i.e., at any position \(i\) we can sum up to some further position (that depends on \(i\)), lets call it $J(i)$, such that \(\displaystyle \sum_i^{J(i)} r_i c_i \leq 3\). In the shipping analogy this is like having the shipping yard say you can only move 3 containers out at a time. For a general query limit of \(K\) this would be \(\displaystyle \sum_i^{J(i)} r_i c_i \leq K\).
Dynamic programming
Now that we have a clear description of the problem, we can follow our nose to see what pops out. Let’s try and figure out how to find the minimum first before figuring out what grouping gives us the minimum. It helps to look at some concrete examples. Consider the example where we have 5 days, with the number of records given by \([1,1,0,1,2]\) respectively.

The naive number of calls required is 5 since you would make a call for 1, 1, 0, 1, 2 items for each of those individual days. Just by visual inspection, we can see there are better combinations. For example,

where we query for 1,1,0 in one call, 1 in another, and 2 in the last call, requires only 3 calls, giving us a savings of 2 calls. But similarly, 1, then 1,0,1, then 2 could also work.

In fact, there is often more than one combination that minimises the calls required. After looking at a few more examples, you might start noticing that to calculuate the minimum number of calls at a given point in the array, you can look at groupings of the part of the array up to that point. If you were going to try a brute force approach, there would be an exponential amount of combinations to try. But we can do better than this. Suppose we saved the minimums along the way. Can we use past minimums to calculate the next minimum?
“Those who do not learn history are doomed to repeat it.” - Dynamic Programming, 1957
Our constraints give us some insight. Remember, every query has a maximum number of results that can be returned, so at most we can only look back in the array to an amount not exceeding that limit. Furthermore, if we had the past minimums, we could look at every combination of past minimum, plus the number of calls needed to go from that position to the current position. Note that the number of calls needed to fetch a given number of results is roughly number of records divided by the page limit. Once we have calculated that, we can take the minimum number of calls from that set of numbers to get the minimum for the current position. In our example, the window can only look back to at most 3 records.
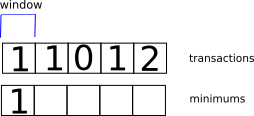


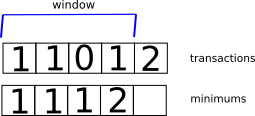
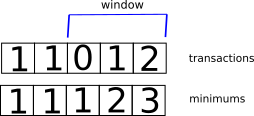
Computing the minimums to the end, we notice that the last element of the array is the minimum number of calls for all the data, in this case the minimum is 3.
Backtracking
So that’s great, we’ve figured out how to calculate the minimums. Note that it is possible to have multiple combinations that get to the final minimum. All we did at each stage was pick one of those combinations that gave the best move at any given point. So how do we actually come up with groupings so that we can save ourselves a lambo? The key is to keep another array of moves we make, and work backwards once we have the solution. In our example, the final minimum of 3 at position 4 (0 indexing), might have come from the minimum at position 3 (with 2 calls), plus 1 more call. So we could record position 3 as the move we made. Then we keep jumping backwards from each move until we reach the start and we can see where we need to group the calls together.
Code
Putting it all together, it might look a little something like:
import sys
from math import ceil
from collections import deque
def num_calls(num_results, max_per_call):
return ceil(float(num_results) / max_per_call)
def extract_groups(moves):
groups = list()
j = len(moves) - 1
while j >= 0:
i = moves[j]
period = (i, j)
groups.append(period)
j = i - 1
return reversed(groups)
def optimise(max_per_call, max_per_query, counts):
n = len(counts)
if n == 0:
raise Exception('Empty counts received')
if n == 1:
return counts, num_calls(counts[0], max_per_call)
min_calls = [sys.maxsize] * n
moves = [0] * n
min_calls[0] = num_calls(counts[0], max_per_call)
for i in range(1,n):
result_count = 0
min_calls[i] = num_calls(counts[i], max_per_call) + min_calls[i-1]
for j in range(i, -1, -1):
curr_count = counts[j]
result_count += curr_count
if result_count > max_per_query:
break
candidate = num_calls(result_count, max_per_call)
if j-1>=0:
candidate += min_calls[j-1]
if candidate <= min_calls[i]:
min_calls[i] = candidate
moves[i] = j
groups = extract_groups(moves)
return groups, min_calls[-1]
groups, min_calls = optimise(2, 3, [1,1,0,1,2])
print(min_calls) # 3
print(list(groups)) # [(0,1), (2,4)]
Complexity
Since we are looking back to at most 3 results, you could reasonably guess that the worst case complexity is \(O(N)\), or \(O(KN)\) in general. This is true if every element in the array is greater than 0. But if we allow for periods with 0 records like in our example, it could potentially keep looking back. This leads to a worst case complexity of $O(N^2)$.
Final thoughts
We have looked at looked at how one might save a few lambos by minimising here and there, however mileage may vary depending on how the records are spread out. In the worst case, you don’t save anything, and at the other extremely, you could save potentially close to 100% depending on the parameters (we have seen a 66% saving example). But it’s not all bad for the service provider. Less API calls also means less bandwidth costs. It do be like that sometimes.
I will end by pointing out that we have looked at an ‘offline’ version of the problem where the distribution of records is known beforehand. If you need to calculate it without this metadata, you will be dealing with the online problem where you will need to live with having weaker performance guarantees (approximate bounds).
– Banner photo by CHUTTERSNAP on Unsplash